前言
之前“抄题解” (emm也不完全是),反正就是没弄懂照葫芦画瓢写了线段树。
这回就来真的写一篇博客记录下学线段树的过程(树状数组现在看起来有点简单了,就是树状数组给的信心,希望不要被线段树搞没了)
经典用法
给定包含 n 个数的数组 a ,有两种操作
- 给区间 [l,r] 中的数增加 x .
- 查询区间 [l,r] 中数的最大值.
线段树是什么
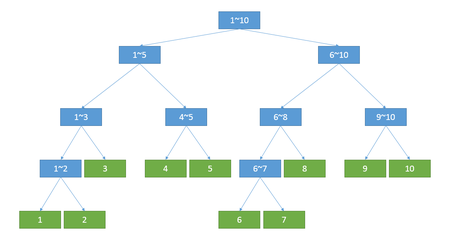
在线段树中,每个节点表示的区间由以下规则确定:
- 根节点表示的区间为 [1,n].
- 若一个点表示区间为 [l,r],且l ≠ r,则其有两个子节点,取m=向下取整((l+r)/2),左儿子表示 [l,m],右儿子表示 [m+1,r]
很显然,这有点分治思想,可以理解为分治思想在log₂n复杂度下的树化。又因是一个二叉树,所以树高(log n)【每层节点的区间长度是上一层的一半】。整个二叉树节点数为2n-1,这里是二叉树的一个性质:
- 线段树底层有 n 个点
- 每合并2个点需要增加1个点
- n个点需要合并 n-1 次,所以一共 2n-1 个点
常用的编号方法:根节点为1,x的左儿子是 2x ,右儿子编号为2x+1。
注意:采取这种编号方法需要开4n的空间
线段树怎么做
单点修改:将该点位置的值修改后,向上更新
单点查询:从上往下找,类似于单点修改,找到后返回
区间查询:寻找尽可能少的不相交区间使其并集为 [l,r]。同样也是从上往下找。
区间查询和区间修改中,绿色的点代表和我们需要查询的区间有交集,而红色的点代表我们直接将这个点的信息取走了,下面是区间查询和区间修改的部分代码。
#define ll long long
#define update v[k]=v[k<<1]+v[k<<1|1]
void pushdown(int x){
v[x<<1]+=len[x<<1]*lazy[x];
v[x<<1|1]+=len[x<<1|1]*lazy[x];
lazy[x<<1]+=lazy[x];
lazy[x<<1|1]+=lazy[x];
lazy[x]=0;
}
ll query(int l,int r,int ql,int qr,int k){
if(l==ql&&r==qr)return v[k];
if(lazy[k])pushdown(k);
int mid=l+r>>1;ll res=0;
if(ql<=mid) res+=query(l,mid,ql,min(qr,mid),k<<1);
if(qr>mid) res+=query(mid+1,r,max(ql,mid+1),qr,k<<1|1);
return res;
}
void modify(int l,int r,int ql,int qr,int k,int y){
if(l==ql&&r==qr){
v[k]+=len[k]*y;
lazy[k]+=y;
return;
}
if(lazy[k])pushdown(k);
int mid=l+r>>1;
if(ql<=mid) modify(l,mid,ql,min(qr,mid),k<<1,y);
if(qr>mid) modify(mid+1,r,max(ql,mid+1),qr,k<<1|1,y);
update;
}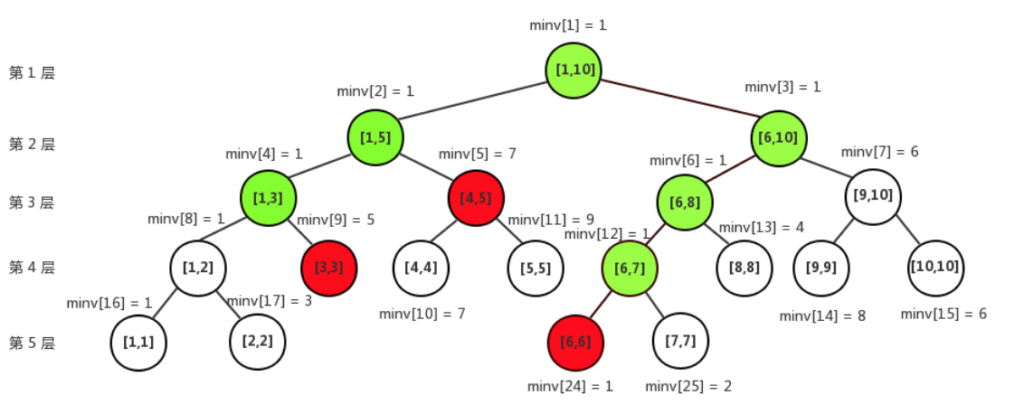
在这张图里面,每行绿色/红色的点均不超过两个:
- 在同一行绿色的点超过两个:以第2层为例,显然我们要求得的区间是与左节点(2号)的右边有交集和右节点(3号)的左边有交集,如果第3层出现3个绿色的,显然无法满足以上条件。
- 在同一行红色的点超过两个:以第4层为例,如果5号节点变为绿色,9、10号节点是红色的,那我们讨论三种情况:
- 1.若8号节点是红色,那么4号节点就应该是红色了,不成立
- 2.若11号节点是红色,那么5号节点就应该是红色了,不成立
- 3.若不是8号节点也不是11号节点,其他的节点是红色的集合中间就出现了不连续的问题,不成立
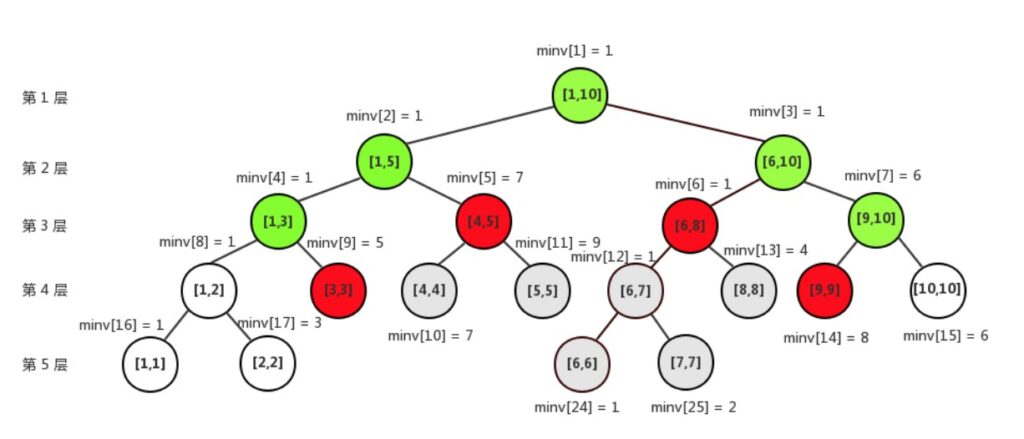
区间修改(要加上许多麻烦操作了):与区间操作的节点相同。若我们仅修改红色节点,灰色节点的值不正确。我们在红色节点处打上标记,经过时下传——懒标记。在红色节点打标记的目的就是为了保证复杂度,红色的点跟上图表示的意思是一样的,换种说法就是红色节点的集合一定是要查询的区间集合的子集。打上lazy tag后就保证了每次操作的时间复杂度是O(log n)
zkw 线段树
特点:
- 自底向上访问节点的线段树
- 非递归,效率高,代码稍短、
- 缺点:需要把树变成的完全二叉树。容易出错,部分功能不易实现,不能下放标记,需要标记永久化
- 标记永久化:标记不会改变,从下往上走时遇到标记的时候就直接计算进去
树套树
- 二维树状数组/二维线段树——例如维护一个矩形区域的和/最大值
- 线段树 + 平衡树(比较常用)
- 线段树 + 前缀和(主席树)
- 线段树 + 树状数组(可修改主席树)
- kd-tree 堆 ······
hhhhhhhhhhhh