前言
就是说经历的太少,之前无法Get到树状数组的点并且一味的被灌输知识。这次来主动重新研究一遍树状数组究竟是什么?
- 用于高效维护前缀信息
- 需要满足信息的高效合并
- 例子:两个子区间的最大值取Max就是整个区间的最大值
- 维护区间信息需要满足信息可减
- 例子:知道一个区间的和且知道其中一个子区间的和,就可以知道另一个区间的和
- 反例:反之知道一个区间的最大值和一个子区间的最大值,并不能确定另一个子区间的最大值
lowbit
这是在树状数组中必须要会的东西,定义为:对于一个正整数 x ,定义lowbit(x)为 x 的二进制表示中最右边的1所对应的位置(值)。
即lowbit(x) = x&-x
比如:
- 6=110₂ ->lowbit(6)=2
- 4=100₂ ->lowbit(4)=3
为什么是对的?首先我们要介绍二进制的表示方式:原码、反码、补码
在正数中,原码反码补码都相同
例如用6位二进制表示一个数,那么6=000110₂
那-6的反码就是111001,负数的补码是反码+1,即-6=111010₂(反码)
这里还出现一个奇怪的现象,因为0和-0在反码中可以被重复表示
- 111111₂=0
- 000000₂=0
所以计算机中反码的表示范围会比补码少1个,为了实现资源利用最大化,计算机就会用补码来存数(反码是一个方便定义补码的螺丝钉呢)
那为什么 x&-x 是对的?
我们可以很容易想到,对于6=000110₂,它的反码是6=111001,补码是111010,相当于补码加的1正好可以使补码右边的1变成0,直到找到与原码从右往左数的第一个1的位置。即lowbit(6)=2
在树状数组中,节点 i 表示的区间为 [i – lowbit(i)+1,i]

此图有以下性质
- 同层节点表示区间不相交
- 左儿子表示区间为父亲的子集
- 右儿子表示区间和父亲不相交
- 奇数的lowbit都为1
为什么树状数组能优化复杂度?
例如我们需要修改 x -> 修改包含x的所有区间
- 从 x 点往上走
- 若当前点是左儿子,则父亲节点包含x
- 反之若当前点是右儿子,则父亲节点不包含x
修改时:寻找第一个大于 x 且是 x 祖先的数
显然这个条件不够 => 我们要寻找最小的大于 x 且 lowbit 大于 x 的数 相当于我们不会往右子树走
怎么快速让我们找到第一个lowbit比 x 大的数呢?
我们回到6=000110₂这个数来看,我们要让lowbit变大,那肯定只能加一个数(减一个数就变小了就不满足条件了不是?),我们要加的数还要尽可能小,那我们干脆直接加一个lowbit完事了!回到例子来看,就是加了一个lowbit(6)=2,刚好可以让这个数的lowbit变大!
修改完下一步是查询:我们寻找若干不相交的区间使其并集为[1,x]
- 首先取出以 x 结尾的区间 [x – lowbit(x) +1,x]
- 则只需要求[1,x – lowbit(x)]的区间 相当于在树上不断向左走
查询和修改刚好相反,是一个很优美的算法。一个是加lowbit一个是减去lowbit
时空复杂度说明:
- 树高为O(log₂ n)
- 修改和查询均只会使用每层最多一个点——每次加减一个lowbit
- 故时间复杂度均为 O(log n)
- 空间复杂度 O(n)——只用存每个节点的信息即可
常见用法
单点加法,查询区间和:
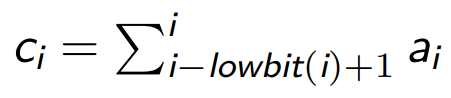
核心代码极其简单:
void update(int x,int y){
for(;x<=n;x+=(x&-x)) tree[x]+=y;//累加加上去
}
int Ans(int x){
int s=0;//求答案 类似于前缀和
for(;x;x-=(x&-x)) s+=tree[x];
return s;
}我们要在上面做一些变形
- 将 tree[x] 修改为y——update(x,y-tree[x]);
- 查询区间 [l,r]的和——Ans(r) – Ans(l-1);
- 查询 x 点的值——Ans(x);
另一种变形是区间加减法,我们会用到“差分思想”
- 区间加法,查询单点值
inline int query(int x){
int s=0;//用符号描述不易懂,这里采用代码描述
for(;x>0;x-=x&-x) s+=tree[x];
return s;
}- 令区间 [l,r] 加上y——update(r+1,-y);update(l,y);
- 查询 x 点的值——Ans(x)
树状数组到此基本就结束了,简单易懂(当然初次接触这个概念会有恐惧感,但整篇文章篇幅其实并不长呢!)
这里放一个拓展用法,拓展用法就不讲了咯!(过于麻烦了还是晚点学线段树吧)
